先来看个老套的例子，斐波那次序列：0,1,1,2,3,5,8,13,21后一个数等于前两个数的和。 如果求第n个数是几？

动态规划

按照常理的计算方式，就是从左到右依次求和就可以得到n， 即：f(0)+f(1)=f(2)，然后f(1)+f(2)=f(3)一直到f(n-2)+f(n-1)=f(n) 用Golang代码实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func FibonacciWithFor(n int) int {
	if n==0 {return 0}
	pre:=0
	next:=1
	for i := 1; i < n; i++ {
		sum:=pre+next
		pre=next //把后一个值给到前一个便于后一轮计算
		next=sum
		//fmt.Println("i:",i,"pre:",pre,"next:",next)
	}
	return next
}

其中定义前后两个变量，依次代表f(n-2)和f(n-1)的值。 这种安装人脑常理的计算方式就是 动态规划 了,那么我们再看如果是计算机思维的解答方式 递归

递归

既然f(n)=f(n-1)+f(n-2)，那么f(n-1)呢，是不是就等于f(n-1)=f(n-1 -1)+f(n-1 -2)，这里我故意用空格隔开了后边的一个减号，意思就是这里的n-1可以看成一个整体 用 n 代替 n-1 ，就成了f(n)=f(n-1)+f(n-2)。从数学公式上来说就是同一个函数，也就是说f(n-1)的子问题可以用和f(n)一样的方法解决。

暴力递归

先来看看代码如何实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

func Fibonacci(n int) int {
	if n==0{return 0}
	if n==1{return 1}
	return Fibonacci(n-1)+Fibonacci(n-2)
}
//测试方法
func TestFibonacci(t *testing.T) {
	fmt.Println("Fibonacci 0:",Fibonacci(0)) //Fibonacci 0: 0
	fmt.Println("Fibonacci 1:",Fibonacci(1)) //Fibonacci 1: 1
	fmt.Println("Fibonacci 10:",Fibonacci(10))//Fibonacci 10: 55
}

代码很像公式且测试方法能得到正确的结果。 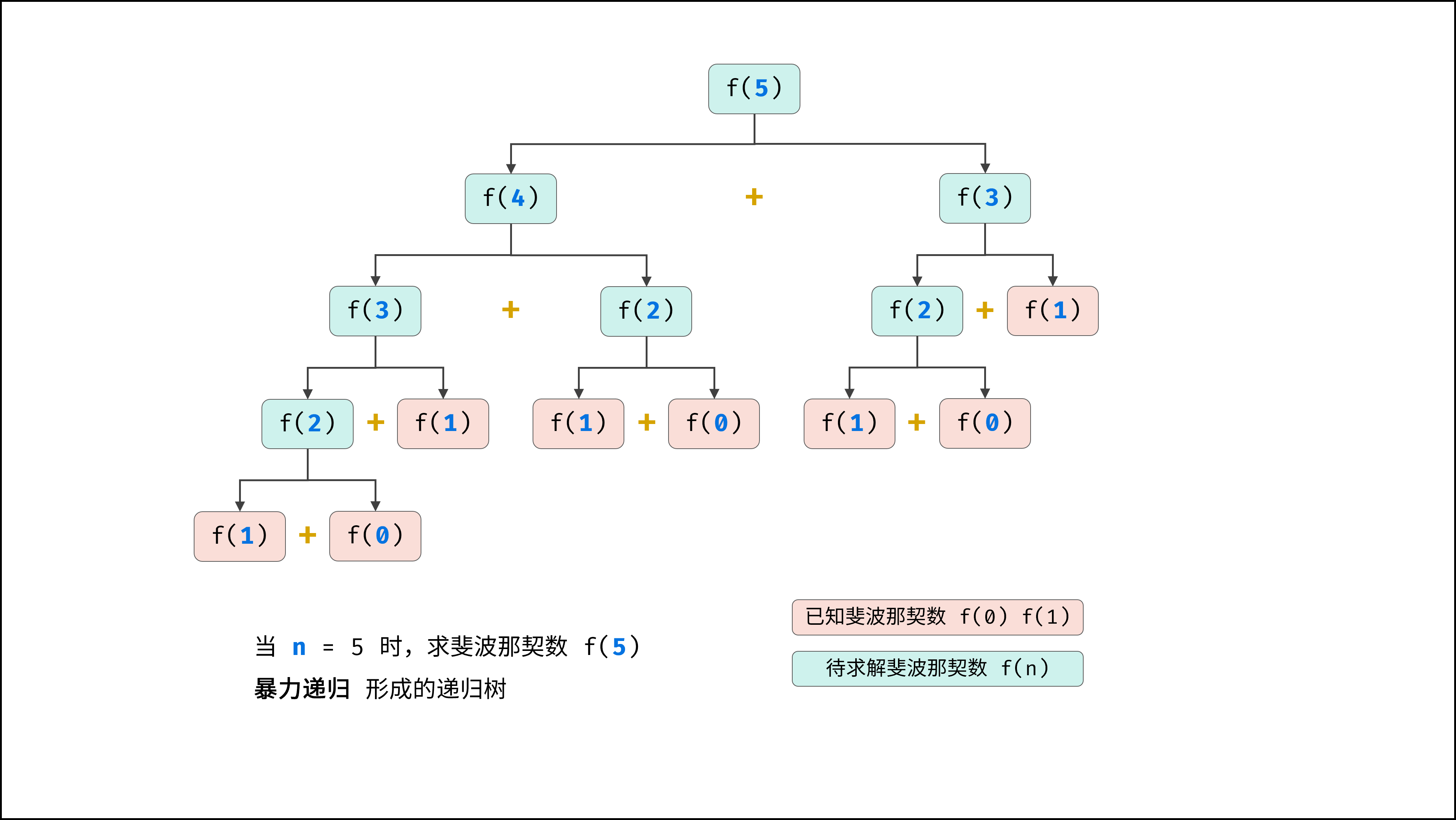暴力递归图1 如图，其中f(0),f(1)…f(n-2)等都被重复计算了多次，虽然函数写起来简单但有好多的重复计算，能否避免呢？

记忆化递归

当然可以。用一个数组保存计算过的f(n-2),f(n-1)不就可以了，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

func FibonacciWithCache(n int,dp []int) int {
	if n==0{return 0}
	if n==1{return 1}
	if dp[n]!=0{return dp[n]}
	dp[n]= FibonacciWithCache(n-1,dp)+ FibonacciWithCache(n-2,dp)
	//fmt.Println("dp:",dp,"n:",n)
	return dp[n]
}

func FibonacciMa(n int) int {
	dp:=make([]int,n+1)
	return FibonacciWithCache(n,dp)
}
//测试方法
func TestFibonacciWithCache(t *testing.T) {
	fmt.Println("FibonacciWithCache 0:",FibonacciMa(0))
	fmt.Println("FibonacciWithCache 1:",FibonacciMa(1))
	fmt.Println("FibonacciWithCache 10:",FibonacciMa(10))
}

你可以打开FibonacciWithCache中的输出可以看到dp数组的变化过程，最后的dp是dp: [0 0 1 2 3 5 8 13 21 34 55],值得注意的是 因为递归的是n所以数组的长度需要比n多一个，避免索引溢出。

总结

记忆化递归和动态规划的本质思想是一致的，是对斐波那契数列定义的不同表现形式：

  • 记忆化递归 从顶至低： 求 f(n)f(n) 需要 f(n - 1)f(n−1) 和 f(n - 2)f(n−2) ； \cdots⋯ ；求 f(2)f(2) 需要 f(1)f(1) 和 f(0)f(0) ；而 f(1)f(1) 和 f(0)f(0) 已知；
  • 动态规划 从底至顶： 将已知 f(0)f(0) 和 f(1)f(1) 组合得到 f(2)f(2) ；\cdots⋯ ；将 f(n - 2)f(n−2) 和 f(n - 1)f(n−1) 组合得到 f(n)f(n) ；

斐波那契数列问题不包含「最优子结构」，只需计算每个子问题的解，避免重复计算即可，并不需要从子问题组合中选择最优组合。 如果想进一步了解，请移步Krahets写的的最优子结构示例：蛋糕最高售价